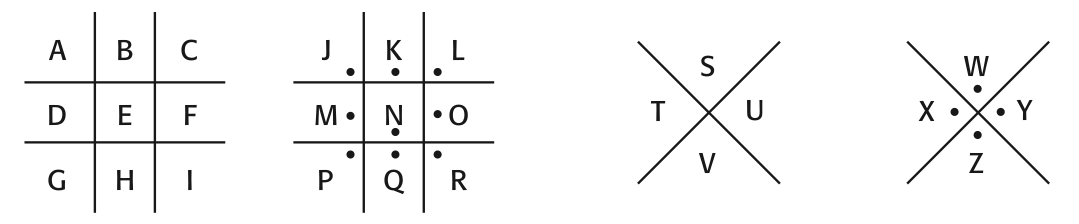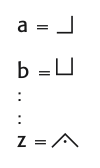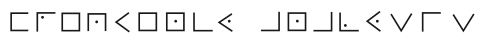频率分析的一些实用技巧
本篇尝试将对西蒙·辛格 The Cook Book 附录部分进行翻译,中文版《密码故事》并未将其一并翻出。
附录一 The Opening of A Void
作者:Georges Perec
翻译:Gilbert Adair
Today, by radio, and also on giant hoardings, a rabbi, an admiral notorious for his links to masonry, a trio of cardinals, a trio, too, of insignificant politicians (bought and paid for by a rich and corrupt Anglo-Canadian banking corporation), inform us all of how our country now risks dying of starvation. A rumour, that’s my initial thought as I switch off my radio, a rumour or possibly a hoax. Propaganda, I murmur anxiously—as though, just by saying so, I might allay my doubts—typical politicians’ propaganda. But public opinion gradually absorbs it as a fact. Individuals start strutting around with stout clubs. “Food, glorious food!” is a common cry (occasionally sung to Bart’s music), with ordinary hard-working folk harassing officials, both local and national, and cursing capitalists and captains of industry. Cops shrink from going out on night shift. In Mâcon a mob storms a municipal building. In Rocadamour ruffians rob a hangar full of foodstuffs, pillaging tons of tuna fish, milk and cocoa, as also a vast quantity of corn—all of it, alas, totally unfit for human consumption.
First published in France as La Disparition by Editions Denöel in 1969, and in Great Britain by Harvill in 1994. Copyright © by Editions Denöel 1969; in the English translation © Harvill 1994. Reproduced by permission of the Harvill Press.
附录二 频率分析的一些实用技巧
- 首先计算密文中所有字母出现的频率。约有5个字母的频率低于 1%,它们可能表示 j, k, q, x 和 z。其中有一个字母的频率应该大于 10%,它可能是 e。如果密文不遵从这条分布规律,那么应当考虑原始信息不是采用英文写作的可能性。你可以通过分析密文字母频率分布来确定一种语言。典型地是意大利语,它的三个字母出现频率高于 10%,9 个字母频率低于 1%。德语中字母 e 的频率高达 19%,因此密文中有如此高频率的字母很可能就是德语。一旦你确定了某种语言,你应该使用合适的频率表对这种语言进行频率分析。只要你使用了恰当的频率表,就很有可能解密以不熟悉语言写成的密文。
- 如果密文显示与英语有联系,但明文却没有立即显现出来——这很寻常——接下来关注几对重复字母。在英语中,最常见的重复字母是 ss, ee, tt, ff, ll, mm 和 oo。如果密文中包含重复字母,你可以假设他们是上面的其中一个。
- 如果密文在单词之间包含空格,那么尝试确定一二或三字母的单词。单字母的词只有 a 和 i。最常见的两字母单词有 of, to, in, it, is, be, as, at, so, we, he, by, or, on, do, if, me, my, up, an, go, no, us, am。最常见的三字母单词有 the 和 and。
- 如果可能,对你正在尝试解密消息的频率表进行删减。比如,在军事消息中倾向于省略代词和介词,诸如 l, he, a 和 the 的缺失会降低某些最常见字母出现的频率。如果已经知道要处理的是军事消息,你应该使用由其他军事消息生成的频率表。
- 对于密码破译师来说,最有用的技巧是根据经验或是知道不完全信息的基础上确定单词,甚至整个短语。海利勒(Al-Khalīl),这位阿拉伯早期的密码破译师,在破解希腊文密文时就展示了这种天赋。他猜测密文是以问候语“以上帝的名义”(In the name of God)开头的,在建立起这些字母与特定密文的关联后,他就可以拿它们用作撬棍,把剩余密文撬开了,就像剽窃他人著作一样。
附录三 言过其实的“圣经密码”
1997年,迈克尔·德罗斯宁(Michael Drosnin)所著的《圣经密码》(The Bible Code)成为了世界各地的头版头条。德罗斯宁声称在圣经中含有隐藏信息,它可以通过搜索“等距字母序列”(equidistant letter sequences, EDLSs)找到。 EDLSs 可以在任意文本中选取特定的起始字母,然后每次跳跃特定数目字母的方式找到。比如说,这个段落是以 Michael 的 M 开头,本例中每次跳五个位置。如果我们以每五个字母跳跃,得到了 EDLS 序列 mesahirt……
即使这个特别的 EDLS 并不含有意义的单词,但德罗斯宁发现了令人惊讶的一系列圣经 EDLSs,它不只是有意义的单词,甚至是完整的句子。由于圣经是如此之大,这不足以说服怀疑论者:在足够大的文本中,通过调整起始位置和跳跃距离而产生的短语不足为奇。澳大利亚国立大学的布兰登·麦凯(Brendan McKay)试图通过在《白鲸记》(Moby Dick)搜索 EDLSs 来证明德罗斯宁方法的必然性,结果发现了十三个有关名人暗杀的叙述,他们包括托洛茨基(Trotsky),甘地(Gandhi)以及罗伯特·肯尼迪(Robert Kennedy)。
附录四 猪圈密码
单字母替换密码(monoalphabetic substitution cipher)以广泛的形式存在了数个世纪。比如,18世纪共济会成员(Freemasons)使用猪圈密码(pigpen cipher)保护其记录的私密。这种密码不使用字母替换另一个字母,而使用符号进行替换。
要加密字母,首先找到它在方格中的位置,然后画出代表那个字母的方格部分。因此:
如果你知道密钥,解密猪圈密码很简单。否则,它会断裂成:
附录五 RSA 的数学原理
- Alice 选取两个大的质数 $p$ 和 $q$. 质数应当尽可能的大,但为了简化说明,我们假设 Alice 取 $p=17$, $q=11$. 她必须对这两个数字保密。
- Alice 将它们相乘得到新数字 $N$. 在本例中 $N=187$. 现在她选取新数字 $e$, 在本例中她取 $e=7$( $e$ 和 $(p-1) \times (q-1)$ 应当互质,但这是技术性的)。
- 现在 Alice 可以将 $e$ 和 $N$ 发表在类似电话簿的地方。由于这两个数字是加密的必要条件,它们必须能被想要给 Alice 发送加密消息的人获取到。这两个数字合称公钥。( $e$ 也可以是其他人公钥的组成部分,就像它是 Alice 公钥组成部分一样。然而,其他人必须有着不同的 $N$ 值,它取决于 $p$ 和 $q$ 的取值。)
- 加密的消息首先要转换成数字 $M$. 比如,一个单词可以转换成 ASCII 二进制数字,二进制数字可以被转换成十进制。根据公式 $C=M^{e}\ (mod\ N)$, $M$ 被加密成密文 $C$.
- 假设 Bob 想要给 Alice 发送一个小玩意:字母 $X$. 在 ASCII 中它被表示为 1011000, 等于十进制 88. 因此 $M=88$.
- 要加密这条消息,Bob 查找了 Alice 的公钥,找到 $N=187$, $e=7$. 这提供了他给 Alice 发送加密消息的加密等式所需要的信息. 由 $M=88$, 可知等式 $C=88^{7}\ (mod\ 187)$.
- 直接在计算器计算是很困难的,因为它无法显示如此大的数字。然而,幂模运算(exponentials in modular arithmetic)中有一个技巧,因为我们知道 $7=4+2+1$,
$88^{7}\ (mod\ 187) = [88^{4}\ (mod\ 187) \times 88^{2}\ (mod\ 187) \times 88^{1}\ (mod\ 187)]\ (mod\ 187)$
$88^{1} = 88 = 88\ (mod\ 187)$
$88^{2} = 7744 = 77\ (mod\ 187)$
$88^{4} = 59969536 = 132\ (mod\ 187)$
$88^{7} = 88^{1} \times 88^{2} \times 88^{4} = 88 \times 77 \times 132 = 894432 = 11\ (mod\ 187)$
现在 Bob 可以发送密文 $C=11$ 给 Alice。
- 我们已经知道幂模运算是一种单向函数(one-way functions),因此从 $C=11$ 反过来恢复到原始消息 $M$ 是很困难的,Eve 无法解密消息。
- 但 Alice 可以,因为她得到了某个特别的消息:她知道 $p$ 和 $q$ 的取值。她计算一个特别的数字,解密密钥 $d$, 它也被称为私钥。数字 $d$ 的计算遵从以下等式:
$e \times d = 1\ (mod\ (p – 1) \times (q – 1))$
$7 \times d = 1\ (mod\ 16 \times 10)$
$7 \times d = 1\ (mod\ 160)$
$d = 23$
(计算 $d$ 的值并不容易,但是辗转相除法(Euclid’s algorithm)能够让 Alice 又快又准地找到 $d$.)
- 要解密消息,Alice 使用这个等式:
$M = C^{d}\ (mod\ 187)$
$M = 11^{23}\ (mod\ 187)$
$M = [11^{1}\ (mod\ 187) \times 11^{2}\ (mod\ 187) \times 11^{4}\ (mod\ 187) \times 11^{16}\ (mod\ 187)]\ (mod\ 187)$
$M = 11 \times 121 \times 55 \times 154\ (mod\ 187)$
$M = 88 = X$ in ASCII
Rivest, Shamir 和 Adleman 创造了一种特殊的单向函数,只有拥有特殊信息(即 $p$ 和 $q$ 值)的人才能执行其逆运算。通过选取 $p$ 和 $q$,他们相乘等于 $N$,得到特定的函数。
为了清楚地阐明要点,我们已经逐字逐句地解释了 RSA 加密消息的过程。在前面的例子中,RSA 有效地解决了单字母替换密码的密钥分发问题。在实际中,加密会使用巨大的二进制数字块进行计算,这使得频率分析成为不可能。
—The Code Book by Simon Singh 青少版 附录补译,原作所使用许可证 Attribution-Noncommercial-No Derivative Works 3.0。
后记 到底谁在公交车上
《密码故事》第68页中译者将 The Sun and the Man in the Moon 翻译成“在月亮中的太阳与人”,这引出了一个有意思的话题。为了说明这个问题,我引用《英语常见问题解答大词典》的例子:
I saw him on a bus.
我在公交车上看到他。
我看到他在公交车上。
哪种理解是正确的,到底谁在公交车上,还是都在公交车上?事实上我们无从知晓答案,在英文中它无法表达出这一种状况。你只能通过上下文去推测谁在哪里。例如:I saw him on the airplane. 双方要得看到对方必须都在飞机上。回到《密码故事》,根据常识可以知道 The Sun and the Man in the Moon 表达的是“太阳和月亮中的人”而不是“在月亮中的太阳与人”,因为很显然月亮的大小是装不下太阳的。这里我引用解答大词典的一段话作为结尾:
在英语中,有时候我们只能根据逻辑分析来确定句子的语法结构,而无法用语法分析加以证明。这说明英语的语法结构的严密性是有很大缺陷的,所以人们常常把英语称为含糊的语言(ambiguous language)。